Analisi Fondamentale VS Analisi Tecnica
Analizzare e comprendere l’andamento i mercati finanziari è sempre stato assolutamente indispensabile per chiunque volesse investire i propri risparmi.
Articoli con tag: analisi tecnica
ALEXANDER ELDER – COME GESTIRE IL PANICO NEL MERCATO
Questo video estratto da un webinar a pagamento del 26 febbraio tenuto dal Dr. Alexander Elder (autore de “Il nuovo vivere di Trading“) e tradotto da Trading Library, spiega come gestire il panico nel mercato, controllando al meglio i titoli e mercati soffocati dal panico degli investitori!
LEZIONI SULLO SHORT INTEREST
Ci sono diversi numeri che controllo prima di far trading, che sia long o short. Uno di questi è lo “Short Interest” (a volte chiamato anche “short float”).
Una giornata a Mercati Aperti con Paola Gentili
Un corso operativo con Paola Gentili è un evento imperdibile!
E il 16 ottobre Paola Gentili sarà presente alla sala corsi di Trading Library, a Cinisello Balsamo, per un seminario a Mercati Aperti!
L’autrice del libro “Vivere di Mercati – Vi insegno un mestiere” e UGO, l’oscillatore sviluppato dalla stessa Paola, saranno a vostra disposizione per una giornata intera per guidarvi nei meandri dei mercati finanziari, vi aiuteranno a comprendere meglio le situazioni di mercato e ad evitare che l’emotività vi distragga nel prendere le decisioni.
Le iscrizioni al corso di Paola Gentili sono aperte e i posti sono limitati!
La variabile o le variabili di Borsa
Quando analizziamo una serie storica dei prezzi di borsa la prima domanda che spesso ci poniamo è: da cosa dipende l’andamento grafico dei prezzi?
Sappiamo tutti che i prezzi di un’attività finanziaria dipendono da
un’infinità di variabili.
Gli econometristi cercano di spiegare il grado di correlazione dei prezzi mediante una qualsiasi variabile presa singolarmente, coeteris paribus, oppure creano dei modelli più articolati dove il prezzo viene determinato da variabili prese contemporaneamente.
Per quanto questo metodo di applicare la statistica inferenziale
all’economia sia sensato, spesso può nascondere delle insidie.
Per dimostrarlo prendiamo in considerazione un semplice esempio
paradossale proposto da un economista contemporaneo, David Hendry, in merito alla crescita dei prezzi dei beni di consumo riportato nel libro di Francesco Guala dal titolo Filosofia dell’Economia: “Confrontando i dati riguardanti la crescita dei prezzi in Gran Bretagna e quelli riguardanti la quantità
cumulativa di pioggia caduta in Scozia negli ultimi decenni, si scopre che esiste una formidabile correlazione fra queste due variabili. Ma ancora più sorprendente è il fatto che se esaminiamo la correlazione statistica fra la crescita dei prezzi e una variabile apparentemente più plausibile come la quantità di moneta circolante nell’economia britannica, scopriamo che essa è più debole. Tuttavia ovviamente nessuno si sogna di spiegare la crescita dei prezzi con la quantità di pioggia, o viceversa; e nessuno spera che l’inflazione diminuisca nei prossimi anni grazie ai mutamenti climatici globali che affliggono il nostro pianeta”.
Sembra incredibile eppure la spiegazione è molto più semplice di quanto si possa pensare.
Si tratta semplicemente di variabili che crescono in modo abbastanza regolare e nella stessa direzione ma per cause completamente indipendenti.
La stessa cosa dicasi per i prezzi di borsa.
Avendo tempo e voglia potremmo trovare tantissime correlazioni che nulla
hanno a che fare con la logica sottostante i modelli finanziari.
Alcuni studiosi, per provocazione e rigetto dell’econometria, ne hanno
studiate alcune.
Io non sarei così categorico con l’econometria ma sicuramente critico.
Penso che il modo migliore per verificare la correlazione tra i prezzi di Borsa e una variabile (tasso d’interesse, bilancia commerciale, tasso di cambio ecc…) non sia quello di calcolare semplicemente l’R^2, l’eteroschedasticità, la correlazione dei disturbi, la multicollinearità; al contrario sarebbe saggio, secondo il mio modesto parere, verificare una sottostante struttura frattale.
Mi spiego meglio.
Se i prezzi di un indice finanziario salgono sia quando il tasso
d’interesse sale sia quando scende, è probabile che tale variabile non
influenzi l’andamento di Borsa.
Quindi potrei trovare un modello funzionante. Ma attenzione: le “batterie” prima o poi si scaricano e bisogna cambiarle con un altro “modello”.
A meno che la struttura frattale non sia sufficientemente attendibile!
Le medie mobili, il coefficiente di Hurst e la dimensione frattale
Come abbiamo appreso dagli articoli precedenti, la finanza frattale è
molto utile per comprendere le dinamiche del mercato finanziario pur non possedendo potenzialità previsionali ma di timing.
molto utile per comprendere le dinamiche del mercato finanziario pur non possedendo potenzialità previsionali ma di timing.
Al contrario l’analisi tecnica, mediante l’euristica, tenta di individuare quelle figure ricorrenti che possono aiutare (e non garantire) l’analista finanziario.
Secondo il mio modesto parere, indipendentemente dal pensiero di apologeti e detrattori, penso sia possibile trovare un fondo di verità anche nell’analisi tecnica.
Premetto che lo stesso Mandelbrot, l’inventore della geometria frattale, ritiene tale disciplina del tutto inutile.
Personalmente non sono così categorico, pur nel rispetto del pensiero di tutti.
Ad esempio, lo strumento più utilizzato dagli analisti tecnici, la media mobile, si concilia molto bene con i fondamenti della finanza frattale.
La perequazione per media mobile del mercato finanziario non è forse un tentativo di rendere l’andamento dello stesso più “morbido” e meno frastagliato?
È possibile!
Poiché gli analisti tecnici lamentano giustamente i ritardi, ma
soprattutto i falsi segnali delle medie mobili, proverò a suggerire un
criterio che non abbia la pretesa di essere scientificamente inconfutabile ma sicuramente adeguato all’utilizzo più efficiente di questo “indicatore”.
In altre parole, il metodo deve essere considerato un complemento
dell’analisi tecnica e non un sostituto. Prima di tarare il dominio della media mobile converrebbe calcolare il coefficiente di Hurst (H) e di conseguenza la dimensione frattale.
Se H è compreso tra 0,5 e 1 deduciamo che i trend esistono e tendono a persistere e quindi l’utilizzo delle medie mobili, ovviamente per quel mercato, è coerente.
Viceversa, se H fosse 0,5 l’andamento seguirebbe una random walk e quindi sprecheremmo tempo e danaro nell’utilizzo di qualsiasi strumento tecnico, medie mobili incluse.
Ma anche se esistesse la tendenza la nostra media potrebbe darci
ugualmente falsi segnali.
Dobbiamo quindi calcolare il grado di “frastagliatura” o segmentazione del
mercato semplicemente calcolando la dimensione frattale che è dato dalla
seguente relazione: 2-H
Tale ultimo valore, come sappiamo, oscilla tra 1 e 2.
Tanto più sarà vicino a 2 tanto più il mercato, per il principio di
autosimilitudine, sarà frastagliato.
Viceversa se tende ad 1.
Come possiamo notare, la dimensione frattale è diretta conseguenza del
coefficiente di Hurst. Infatti se H fosse uguale a 1 (in un mondo ideale)
l’andamento sarebbe perfettamente lineare.
Purtroppo o per fortuna i mercati funzionano diversamente!
Ricapitolando; la nostra media mobile avrà maggiori “probabilità” di
successo se il nostro H sarà compreso tra 0,5 e 1 e la sua dimensione
frattale sarà vicina a 1.
Tale lavoro può essere fatto egregiamente con il foglio Excel.
Molto semplicemente, senza scomodare gli scienziati, abbiamo trovato una trait d’union tra metodologie consolidate (analisi tecnica ecc.) e metodologie moderne (finanza frattale ecc.).
Il campo è ancora tutto da esplorare…
Definire la dimensione frattale dei mercati
Un altro modo di caratterizzare un frattale è quello di definirne la
dimensione. Tutto ciò ha una grande importanza nello studio dei mercati finanziari, anche perché è finalmente possibile calcolare il grado di irregolarità di un grafico ovvero stabilire la sua dimensione frattale.
dimensione. Tutto ciò ha una grande importanza nello studio dei mercati finanziari, anche perché è finalmente possibile calcolare il grado di irregolarità di un grafico ovvero stabilire la sua dimensione frattale.
Anzitutto dobbiamo come sempre porre le basi per una maggiore comprensione di questa metodologia così ostica ma affascinante.
Il concetto di dimensione di un oggetto è abbastanza familiare. Ad esempio un segmento ha dimensione 1, un quadrato ha dimensione 2 ed un cubo ha dimensione 3.
Se dividiamo un segmento in parti uguali, rimpicciolito di un fattore K=1/, ne consegue, mediante formula inversa, che *K=1.
Il quadrato possiamo dividerlo in =4 parti dove il lato di ognuna di esse è rimpicciolita di un fattore K=1/2. Quindi avremo *K^2=1.
La stessa cosa si può ripetere per una figura tridimensionale: avremo
*K^3=1.
Come possiamo notare l’esponente di K rileva la dimensione.
Ma qual è la dimensione di un oggetto, o meglio di un grafico finanziario, frattale?
Possiamo dimostrarlo in modo logico!
Se il mercato salisse o scendesse ininterrottamente (ovviamente in un mondo ideale) senza mai correggere il suo andamento, sarebbe una linea retta “senza sbavature”, ovvero a dimensione unitaria. Viceversa, se il mercato alternasse un giorno di salita a un giorno di pari discesa (sempre nel nostro mondo ideale), i segmenti di retta “riempirebbero” una superficie, ovvero avrebbero per approssimazione dimensione quadratica
come sotto riportato:
La dimensione frattale
La dimensione frattale è come la virtù: sta nel centro!
Avrete sicuramente intuito che tale dimensione oscilla tra 1 e 2, in
quanto il mercato sale o scende in modo “frastagliato” come si evidenzia nel grafico:
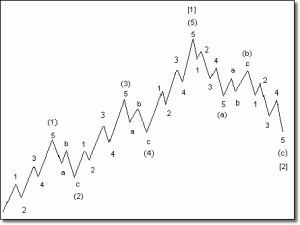
Tanto più sarà irregolare l’andamento tanto più possiamo asserire che la sua dimensione si avvicina a 2.
Se l’andamento sarà perfettamente rettilineo, la sua dimensione sarà uguale a 1.
Senza entrare nei dettagli tecnici, possiamo semplicemente calcolare la dimensione frattale di un’attività finanziaria mediante la seguente formula:
=&0=&
Dove H è l’esponente di Hurst.
Nel prossimo articolo vedremo come risolvere il problema dell’irregolarità di un diagramma finanziario rifacendoci all’analisi tecnica.
Analisi tecnica e finanza frattale
Colgo l’occasione con questo articolo per sfatare un luogo comune:
l’intolleranza della finanza frattale nei confronti dell’analisi tecnica.
l’intolleranza della finanza frattale nei confronti dell’analisi tecnica.
Analizzando nel dettaglio le varie teorie degli analisti tecnici si scopre che l’Ingegnere Ralph Nelson Elliott agli inizi del Novecento intuì l’andamento frattale dei mercati.
Analizziamo un’importante proprietà dei frattali mediante un grafico molto semplice ilustrante l’=&0=&delle figure geometriche irregolari sotto riportate.
La varietà dei frattali è immensa, tuttavia è possibile riconoscere alcune caratteristiche comuni: le parti più piccole sono simili al tutto secondo uno specifico rapporto preciso e misurabile. Nei frattali più semplici, questo rapporto è lo stesso in tutte le direzioni. Tali frattali vengono quindi chiamati =&1=&, e in generale si parla di =&2=&. Sono come “zoom” che dilatano o comprimono nella stessa misura tutto ciò che inquadrano.
Tutto questo non ci ricorda forse la teoria delle onde di Elliott?
Secondo tale teoria un ciclo borsistico primario è scomponibile in tanti sottocicli che mantengono le stesse proprietà del ciclo di partenza come sotto riportato:
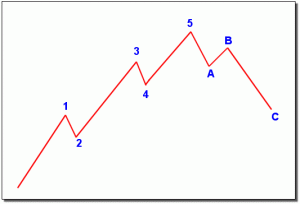
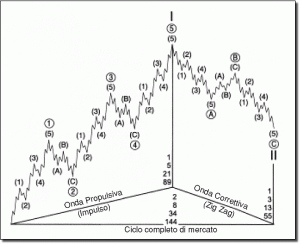
Come possiamo notare un impulso (1), (3), (5), è a sua volta “generato” da altri impulsi e correzioni più piccoli. In altre parole Elliott scoprì l’auto-similitudine dei mercati.
Ed è per questo che possiamo ritenere l’Ing. Ralph Elliott il primo
studioso di finanza frattale, anche se essa come materia nascerà solo più tardi.
Tutto ciò dimostra che quanto stiamo da tempo scrivendo veniva già
utilizzato, anche se inconsapevolmente, dai guru della finanza.
Attualmente la finanza frattale cerca soltanto di dare maggiore
autorevolezza ma soprattutto scientificità al mondo borsistico.
Ad esempio il coefficiente di Hurst si è imposto all’attenzione degli
analisti tecnici come uno strumento più rigoroso per verificare la
presenza di eventuali tendenze.
Saranno i vari oscillatori, medie mobili, figure d’inversione, che
stabiliranno il timing di entrata o uscita dal mercato per gli operatori
ortodossi dell’analisi tecnica.
Come vedete l’analisi tecnica e la finanza frattale non sono affatto
antitetiche (anche se lo stesso Mandelbrot disdegna l’analisi tecnica); al contrario possono essere un potente strumento di minimizzazione del rapporto rischio/rendimento.
Torneremo sull’argomento nei successivi articoli.
La predisposizione dei mercati
Quante volte il nostro trading system non ottimizza i guadagni con
l’utilizzo di una media mobile? In altre parole, quanti falsi segnali
vengono generati prima di mettere in tasca una plusvalenza?
l’utilizzo di una media mobile? In altre parole, quanti falsi segnali
vengono generati prima di mettere in tasca una plusvalenza?
Non pensiate che la media mobile sia lo strumento sbagliato per cavalcare le tendenze di mercato, o che il nostro trading system sia da buttare.
Passatemi l’esempio medico. Le medicine non sono un male in se stesse ma solo se utilizzate per sconfiggere una malattia della quale non sono stati riscontrati sintomi.
Questo accade anche in finanza. Se prima non studiamo la predisposizione del mercato ad ammalarsi di una certa malattia (tendenza o trading range) è inutile curarlo con strumenti inadeguati (RSI o medie mobili).
A ciascun mercato il proprio indicatore!
Anziché testare una miriade di oscillatori, divergenze, ecc. per poi
cadere sotto la scure della legge di Murphy, cerchiamo di agire in modo
più razionale ed economico.
Non continuiamo a lanciare la moneta per scegliere le attività finanziarie che massimizzino il rapporto rendimento/rischio.
In poche parole, studiamo prima la predisposizione dei mercati e solo dopo testiamo gli strumenti più idonei.
Forse non avremo la certezza matematica di diventare ricchi ma sicuramente diventeremo più consapevoli di ciò che può accadere ai nostri soldi. Evento catastrofico e imprevisto a parte. Ma questo rischio lo può controllare soltanto Dio!
Negli articoli precedenti abbiamo osservato come i vari mercati possano essere soggetti a tendenze persistenti, antipersistenti e in un caso specifico a un random walk.
Più precisamente un’attività finanziaria presenta una tendenza persistente quando il coefficiente di Hurst è compreso tra 0,5 e 1; antipersistente quando tale coefficiente è compreso tra 0 e 0,5.
Mentre la random walk theory è spiegata da un coefficiente intorno a 0,5.
Gli studiosi di finanza frattale non escludono la teoria dei mercati
efficienti ma la vedono come un caso particolare di un modello più
generale.
Tenteremo adesso di spiegare l’utilità pratica di tale “strumento”. O
meglio, come H ci indichi la predisposizione di un mercato.
Spesso il problema dell’investitore non è tanto quello di prevedere il
futuro o di capire l’esatto timing del mercato; ma viceversa di sapere
quali strumenti d’analisi utilizzare per avere maggiori probabilità di
sovraperformare il mercato.
In tale contesto l’analisi del coefficiente di Hurst può aiutarci.
Se H è maggiore di 0,5 allora una gestione che utilizza una strategia
attiva, come l’analisi tecnica o l’analisi statistica, può essere
giustificata.
Ad esempio prima di testare una media mobile potremmo calcolarci H. Se questo fosse vicino ad 1 allora possiamo aspettarci una discreta riuscita dall’utilizzazione della nostra media rispetto ad una strategia di tipo passivo. Ovviamente lo stesso discorso vale per molti altri indicatori.
Se il nostro coefficiente si avvicina a 0,5 allora sarebbe più utile una
strategia di tipo passivo del tipo “Buy and Hold”. Il mercato segue un
random walk.
Il problema sorge quando H è compreso tra 0 e 0,5. In questo caso parliamo di “antipersistenza”.
Il mercato oscilla tra due opposti. O meglio, se un giorno è in salita
molto probabilmente il giorno dopo sarà in discesa. Paradossalmente, l’antipersistenza per un analista tecnico o “attivo” è da preferire rispetto a un random walk.
Ovviamente indicatori direzionali come le medie mobile ci darebbero troppi falsi segnali a causa del continuo fluttuare dei prezzi intorno alla media.
Mentre l’utilizzo di algoritmi che segnalano un ipercomprato/ipervenduto (RSI, Stocastico) non sono da sottovalutare. Anche se il dominio deve essere tarato in modo “corretto” e non in modo convenzionale. Torneremo
nei prossimi articoli sull’argomento dell’antipersistenza.
Il mercato è predisposto a “scaricare” subito gli eccessi. Mentre come possiamo intuire l’utilizzo di un RSI con un H prossimo a 1 sarebbe disastroso perché la persistenza della tendenza non può essere sfruttata dagli oscillatori.
Nel libro di Benoit Mandelbrot si legge: «Alcuni studi di Peters rilevano importanti livelli di H per alcune attività finanziarie. Ad esempio Apple sembra avere un H prossimo a 0,75, la Xerox un H=0,73.
Mentre alcuni economisti “svelano” un random walk su diversi cross
monetari. In particolare il rapporto dollaro-dollaro canadese assume
valori molto vicini a 0,5».
Come abbiamo intuito la finanza frattale ci dà una spiegazione generale e necessaria per comprendere quale tipo di strategia abbia maggiori probabilità di riuscita. L’importante è utilizzarla per capire la predisposizione di un mercato.
Ma soprattutto all’interno dell’analisi tecnica ci può indirizzare verso gli algoritmi “giusti”. Non ci rimane che effettuare i test e verificare quanto fin qui descritto.
Buon trading.
L’esistenza di tendenze di mercato persistenti è dimostrabile?
Lungi da me l’intenzione di trattare la questione da un punto di vista
epistemologico.
epistemologico.
Non ho le competenze (e neanche faccio qualcosa per averle) di un filosofo della scienza.
Dobbiamo semplicemente scomodare la statistica.
Proviamo prima a fare un semplice esperimento che nel libro di Benoit Mandelbrot viene spiegato molto bene:
«Quando si gioca a testa o croce, si può avere lo stesso risultato molte volte di seguito, naturalmente, altrimenti nessuno vincerebbe. E la formula è semplice: la differenza tra la massima vincita di Tommaso (il nostro giocatore) in un certo momento
del gioco e la massima perdita in un altro momento varia in proporzione alla radice quadrata del numero dei lanci.
Supponiamo, per esempio, che la partita consista di 100 lanci, che la
massima vincita di Tommaso sia stata 8 e la massima perdita 3. La
differenza è quindi pari a 11. Ora immaginiamo che il gioco sia cento
volte più lungo, quindi che la moneta venga lanciata 10.000 volte. La
formula dice che la differenza dovrebbe essere dieci volte più grande, quindi uguale a 110. La teoria suggerisce che il risultato migliore di Tommaso potrebbe essere 67 e il peggiore -43».
Sembra complicato ma solo in apparenza.
Come il lettore avrà intuito è solo necessario trasportare questo concetto all’andamento dei mercati.
Se il campo di variazione non aumenta in ragione di circa la radice
quadrata di ma con un’altra legge, vuol dire che la nostra moneta (i
prezzi di mercato) è in alcuni casi truccata.
Asserire questo potrebbe significare, in automatico, stabilire che la
sequenza temporale dei prezzi di Borsa non è del tutto casuale ma soltanto caotica.
Allora i prezzi del passato “scaricano” la loro memoria in un arco
temporale prolungato.
In altre parole le tendenze esistono e sono persistenti!
La costruzione dell’algoritmo matematico è stata presa a prestito
dall’idrologia ed in particolare da Edwin Hurst. Il coefficiente di Hurst è proprio ciò che la finanza stava cercando per dimostrare la
“scientificità” delle tendenze di mercato.
La formula si presenta nel seguente contesto che spiegheremo nel minimo dettaglio:
Per la proprietà dei logaritmi possiamo ricavare H nel seguente modo:
Log(R/S)=H*Log(N)+Log(K)
Non ci rimane che analizzare il nocciolo della formula ovvero R/S:
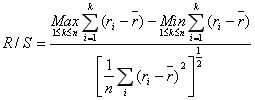
Per sintetizzare il pensiero di Mandelbrot possiamo dire che:
«Una delle caratteristiche principali di questo metodo è che i suoi risultati non dipendono dalla organizzazione dei dati. La formula si limita a misurare se la differenza tra i valori massimi e minimi dei dati è superiore o inferiore a quella prevedibile quando ogni dato non dipende dai precedenti.
Per determinare il numeratore si calcola il rendimento ri dalla variazione di prezzo di un titolo o di un indice in intervalli diversi (uno, due, … giorni) e si confronta con il rendimento medio r sull’intero periodo di giorni. Si esegue il calcolo per un giorno, poi per due e così via fino a determinare il valore massimo e quello minimo di tutte le differenze. La differenza tra questi due valori stima l’intervallo di variazione della serie. Il denominatore è la comune formula della deviazione standard».
Per il calcolo del coefficiente di Hurst non è sufficiente prendere in
toto un intero campione di dati e svolgere i calcoli di R/S.
Si potrebbe fare ma la forzatura verrebbe spinta all’eccesso. Per converso il modello di Edgard Peters sembra trovare un significato “dimostrabile”.
Mi spiego con un esempio.
Supponiamo di disporre di 100 rilevazioni giornaliere sull’indice SPMIB.
Calcolo R/S sulle prime 10 osservazioni. Poi dalla 11 alla 20. E così via. Ne calcolo la media e ottengo un valore di R/S. Questo passaggio, anche se macchinoso, è indispensabile per dare la stessa importanza ai dati dei sottocampioni.
Dopo calcolo R/S sulle prime 20 osservazioni. Poi dalla 21 alla 40. E
attuo lo stesso procedimento sopra descritto.
Poi con 25. E infine con 50.
Alla fine regredisco Log (R/S) su Log (N) e il coefficiente angolare della
retta di regressione non può che restituirmi il valore stimato di H.
In realtà Peters calcola il tutto sui residui ma il discorso si
complicherebbe senza modificare la sostanza del valore di H stimato.
Nella prossima “puntata” vedremo la dimensione frattale dopodiché
posseremo a verificare se essa può funzionare nel trading di tutti i
giorni.